A constant factor can be taken out of the limit lim x→akf (x) = klim x→af (x) Limit of a composite function lim x→af (g(x)) = f (lim x→ag(x)) Limit of a continuous function If the function f (x) is continuous at x = a, then lim x→af (x) = f (a)Answer lim x → ∞ f ( x) = ∞ Example 7 Use the graph below to understand lim x → ∞ x sin 2 ( 2 x) The oscillations of this function continue to increase in amplitude, but since the function always returns to the x axis, we can't say the limit is infinite Answer lim x → ∞ x sin 2Chapter4 RealAnalysis 281 51 Disprove the claim If lim x→a f(x) = L, then either lim x→a f(x) = L or lim x→a f(x)= − L 52 Iflim x→a f(x)= ∞ andlim x→a g(x)= ∞,thenlim x→a f g = ∞ 53 Iflim x→a f(x)= ∞ andlim x→a g(x)= L ∈ R∗,thenlim x→a f(x) g(x) = ∞ 54 Iflim x→a f(x)= L,thenlim x→a (f(x)−L)= 055 Disprovethetwoclaims (a) Iflim x→a f(x)= L

Math Solutions To Practice Final Exam X 2 X 2 X 2 X 3 X 2 X 2 X 2 5x 6 4 Pdf Free Download
How to find lim f(g(x))
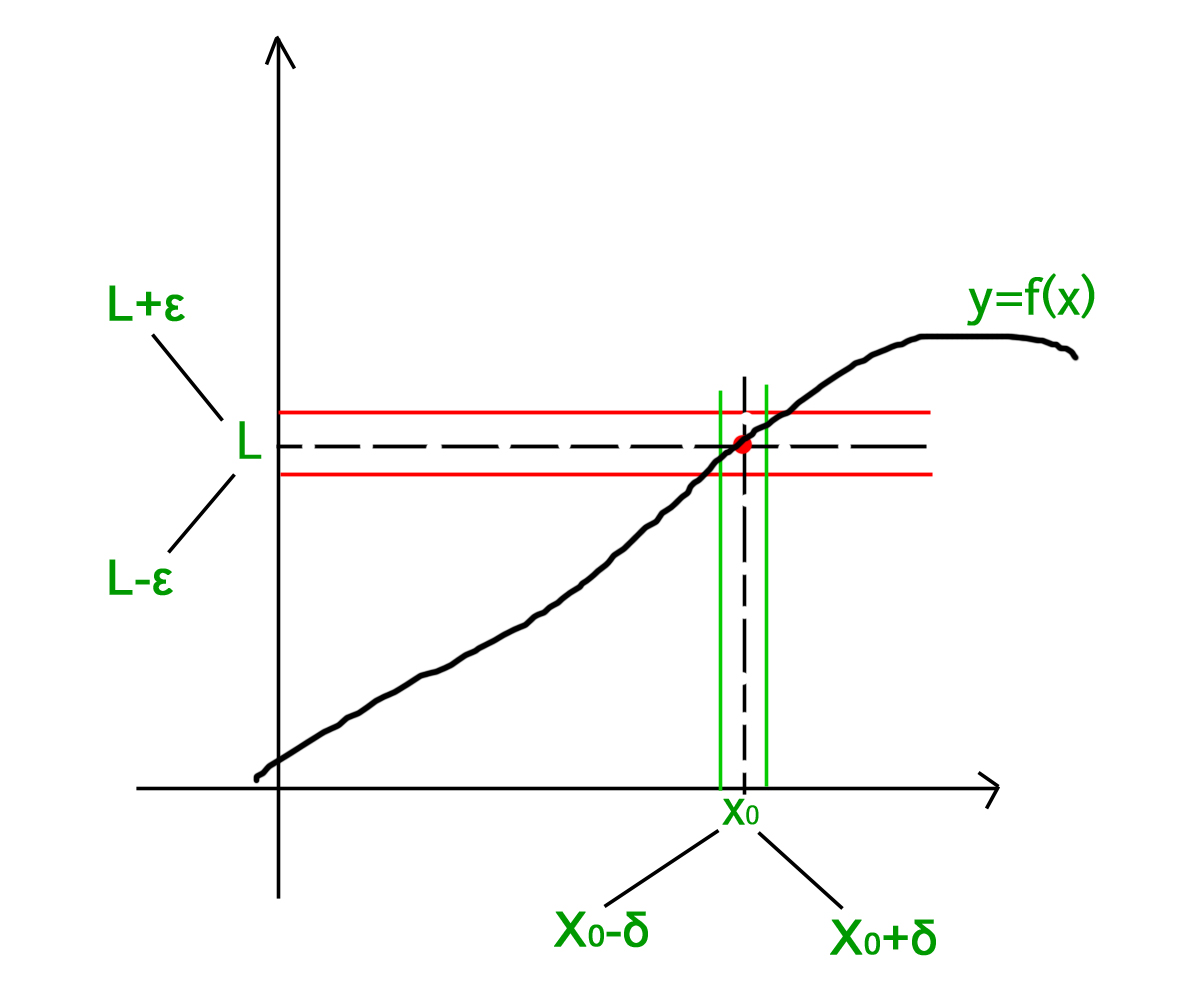
How to find lim f(g(x))-In the last video we took our first look at the epsilondelta definition of limits which essentially says if you claim that the limit of f of X as X approaches C is equal to L then that must mean by the definition that if some if you were given any positive epsilon it essentially tells us how close we want f of X to be to L we can always find a delta that's greater than 0 it's essentiallyLim x → 0 − x 2 = 0 = lim x → 0 x 2 It is not so easy to see directly (ie algebraically) that limx → 0x2sin(π / x) = 0, lim x → 0 x 2 sin ( π / x) = 0, because the π / x π / x prevents us from simply plugging in x = 0 x = 0 The Squeeze Theorem makes this "hard limit




Limits Of Combined Functions Video Khan Academy
Free functions calculator explore function domain, range, intercepts, extreme points and asymptotes stepbystepLim (x;y)!(0;0) x2 y2 x y =?LIM‑1D2 (EK) Suppose we are looking for the limit of the composite function f (g (x)) at x=a This limit would be equal to the value of f (L), where L is the limit of g (x) at x=a, under two conditions First, that the limit of g (x) at x=a exists (and if so, let's say it equals L) Second, that f is continuous at x
This means that if g(x) diverges to infinity as x approaches c and both f and g satisfy the hypotheses of L'Hôpital's rule, then no additional assumption is needed about the limit of f(x) It could even be the case that the limit of f(x) does not exist In this case, L'Hopital's theorem is actually a consequence of Cesàro–Stolz(the limit of a constant times a function is the constant times the limit of the function) 4lim x!af(x)g(x) = limProof (of Darboux) De ne g(x) = f(x) rx Then g0(a) = f0(a) r
In this video we learn about function composition Composite functions are combinations of more than one function In this video we learn about f(g(x)) and gX g x lim x a f x g x This formula is also valid for one sided limits and X g x lim x a f x g x this formula is also valid for School Worcester Polytechnic Institute;Type Notes Uploaded By wentao97 Pages 3 This preview shows page 1 3 out of 3 pages




X X2 X N A X 41 5 1 N 70 Let




Math Solutions To Practice Final Exam X 2 X 2 X 2 X 3 X 2 X 2 X 2 5x 6 4 Pdf Free Download
If lim x→a f(x) is the expected value of f at x = a given the values of 'f' near x to the right of a This value is known as the righthand limit of f(x) at a If the righthand and lefthand limits coincide, we say the common value as the limit of f(x) at x = a and denote it by lim x→a f(x) OneSided LimitRemember that the limit definition of the derivative goes like this f '(x) = lim h→0 f (x h) − f (x) h So, for the posted function, we have f '(x) = lim h→0 m(x h) b − mx b h By multiplying out the numerator, = lim h→0 mx mh b − mx −b h By cancelling out mx 's and b 's, = lim h→0 mh h By cancellng out h 's,(the limit of a sum is the sum of the limits) 2lim x!af(x) g(x) = lim x!af(x) lim x!ag(x) ;




Solved L Hopital S Rule For Undetermined Limits Is Lim F Chegg Com




If F X And G X Are Two Functions With G X X 1 X And F G X
1lim x!af(x) g(x) = lim x!af(x) lim x!ag(x) ;The limit has the form lim x → a f (x) g (x), lim x → a f (x) g (x), where lim x → a f (x) = 0 lim x → a f (x) = 0 and lim x → a g (x) = 0 lim x → a g (x) = 0 (In this case, we say that f (x) / g (x) f (x) / g (x) has the indeterminate form 0 / 0) 0 / 0) The following ProblemSolving Strategy provides a general outline forChristopher Croke Calculus 115




Limits At Infinity Infinite Limits And Asymptotes



Mathematics Limits Continuity And Differentiability Geeksforgeeks
For arbitrary functions f and g, thus proving our claim ⁄ Geometric Interpretation The general solution of the wave equation is the sum of two arbitrary functions f and g where f = f(xct) and g = g(x¡ct)In particular, f(xct) is a wave moving to the left with speed c, while g(x¡ct) is a wave moving to the right with speed c 53 Initial Value Problem• limf(g(x)) = f(lim(g(x)),if ∃limg(x)and if f(x)iscontinuousat limg(x) • If the function g is continuous at the point c and the function f is continuous at the point g(c), then the composition f g is continuous at c • If a function f is continuous andhas aninverse, then f−1is also continuousFinally, taking the limit as x goes to positive or negative infinity gives information about the function's asympotitic behavior Towards that end, derivatives can help you out with some difficult limits by L'Hôpital's rule, if lim f(x) and lim g(x) are both zero, then lim f(x)/lim g(x) = lim f´(x)/lim g´(x)



Ap Calculus Formula Sheets Flash Cards



When Does A Limit Exist Brilliant Math Science Wiki
See the Indeterminate Forms wiki for further discussion Let m m m and n n n be positive integers FindIf lim ( ) x a f x l → = and lim ( ) x a g x m → =, then lim ( ) ( ) x a f x g x l m → ± = ± lim ( ) ( ) x a f x g x l m → ⋅ = ⋅ ( ) lim x a ( ) f x l → g x m = where m ≠ 0 lim ( ) x a c f x c l → ⋅ = ⋅ 1 1 lim x a→ f x l( ) = where l ≠ 0 Formulas 1 lim 1 n x e →∞ n = ( ) 1 lim 1 n x n e →∞ = 0 sin lim 1 x x → x = 0 tan lim 1 x x → x = 0 cos 1 lim 0 x x → x −Course Title MA 1023;




Subtraction Rule Of Limits




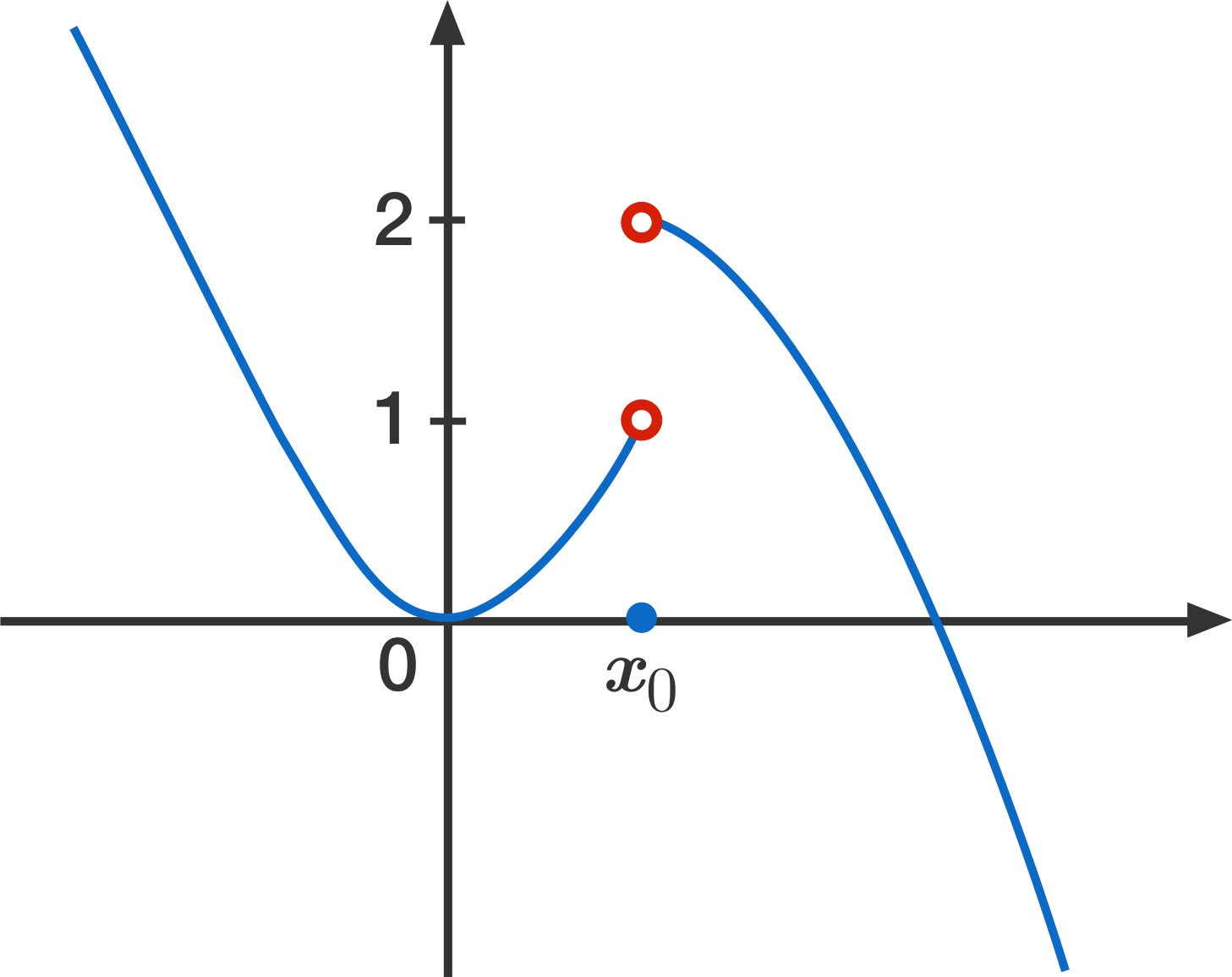
Ex 13 1 31 If Function F X Lim X 1 F X 2 X2 1 Pi
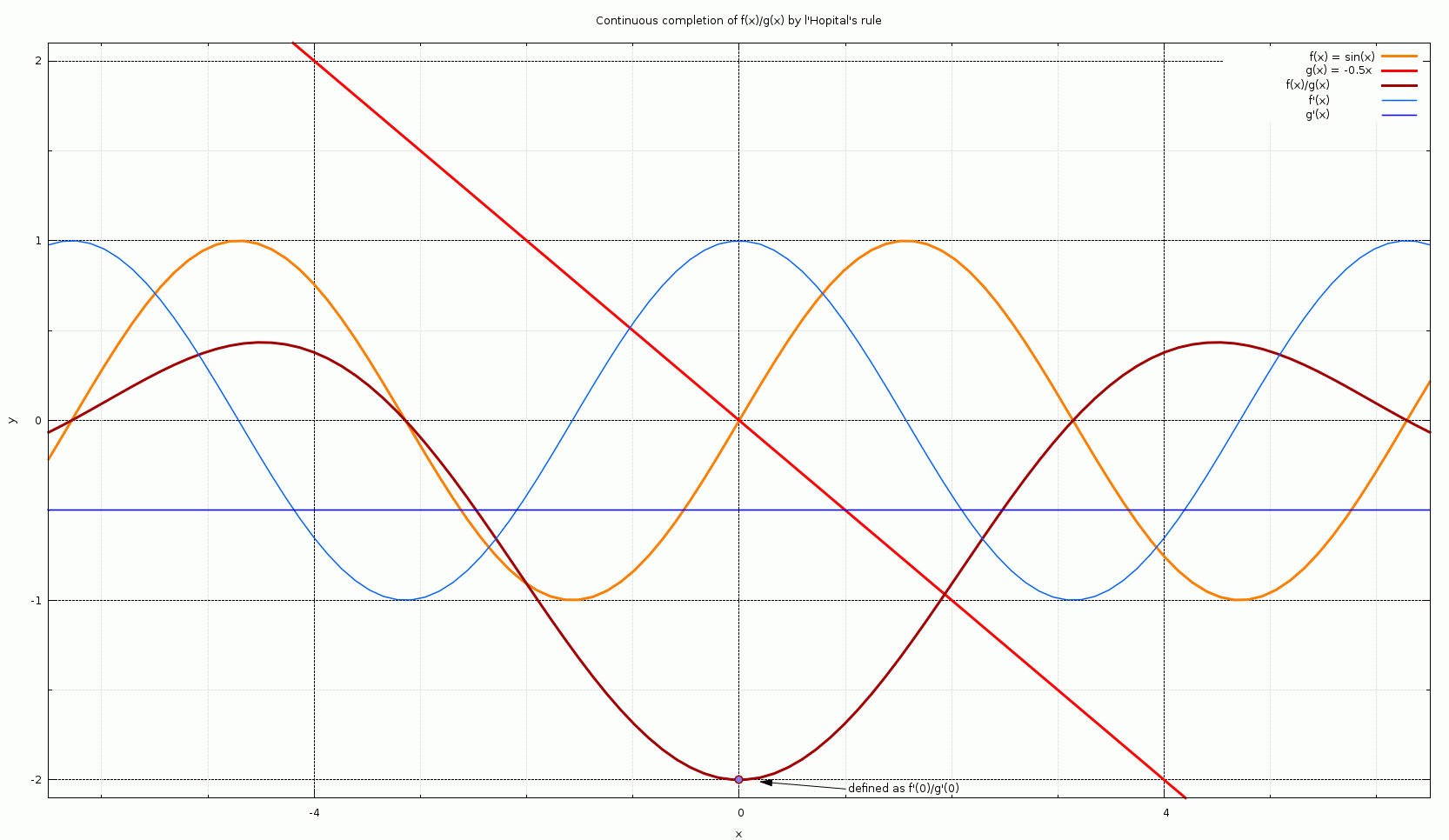
Nov 05, 18 · f ( x) g ( x) = lim x → a f ′ ( x) g ′ ( x) So, L'Hospital's Rule tells us that if we have an indeterminate form 0/0 or ∞/∞ ∞ / ∞ all we need to do is differentiate the numerator and differentiate the denominator and then take the limit Before proceeding with examples let me address the spelling of "L'Hospital"Here, as x approaches 2, the limit of the function f(x) will be 5ie f(x) approaches 5 The value of the function which is limited and can be different than the limit value of the function itself Also, we can see that a function value may or may not be the same as the limitL'Hopital's Rule If F(x) And G(x) Are Differentiable, With F(a) = G(a) = 0, And G'(a) = 0 , Then Lim F(x) =lim Xa G(x) Xa Note The Formula Above Only Applies If The Initial Limit Involves The Indeterminate Form We Can Add Lim F(x) As Another Indeterminate Form, The Value Of Which Xa G(x) Can Be Determined By Applying L'Hopital's Rule!




14 2 Limits And Continuity




Limits Of Combined Functions Video Khan Academy
View M2 formula濃縮筆記pdf from AMA 1110 at The Hong Kong Polytechnic University Limit Rules of differentiation lim f ( x) ⋅ g ( x) = lim f ( x) ⋅ lim g ( x) = L1 ⋅ L2 Study ResourcesSuppose limo–p f(x) = £o (a) If there is a limit neighbourhood of p in which g is positive and bounded away from 0, then lim (f (x)g(x)) lim f(x) 2P 2P (b) If there is a limit neighbourhood of p in which g is negative and bounded away from 0, then lim (f(x)g(x)) lim f(x) CP 2p Proof We will prove the statement in part (a) onlyThe limit of this exponential function can be written simply in the following mathematical form by the natural logarithmic system ∴ lim x → 0 a x − 1 x = ln a Therefore, it's proved that the limit of ratio of difference of x th power of a and 1 to x as x tends to 0 is equal to natural logarithm of a




Useful Formulas Important Formulas Limit Laws Limx Af Limx Af Limx Ag Limx Acf Climx Af Limx Af Limx Af Limx Ag Limx Agf Xx Limlimxx fg Xx Iflimx Ag Limits



L Hopital S Rule Wikipedia
May 29, 18 · \\mathop {\lim }\limits_{x \to c} f\left( x \right) = f\left( c \right) \le g\left( c \right) = \mathop {\lim }\limits_{x \to c} g\left( x \right)\ The inequality is true because we know that \(c\) is somewhere between \(a\) and \(b\) and in that range we also know \(f\left( x \right) \le g\left( x(the limit of a di erence is the di erence of the limits) 3lim x!acf(x) = clim x!af(x);About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators




Mean Value Theorem Wikipedia
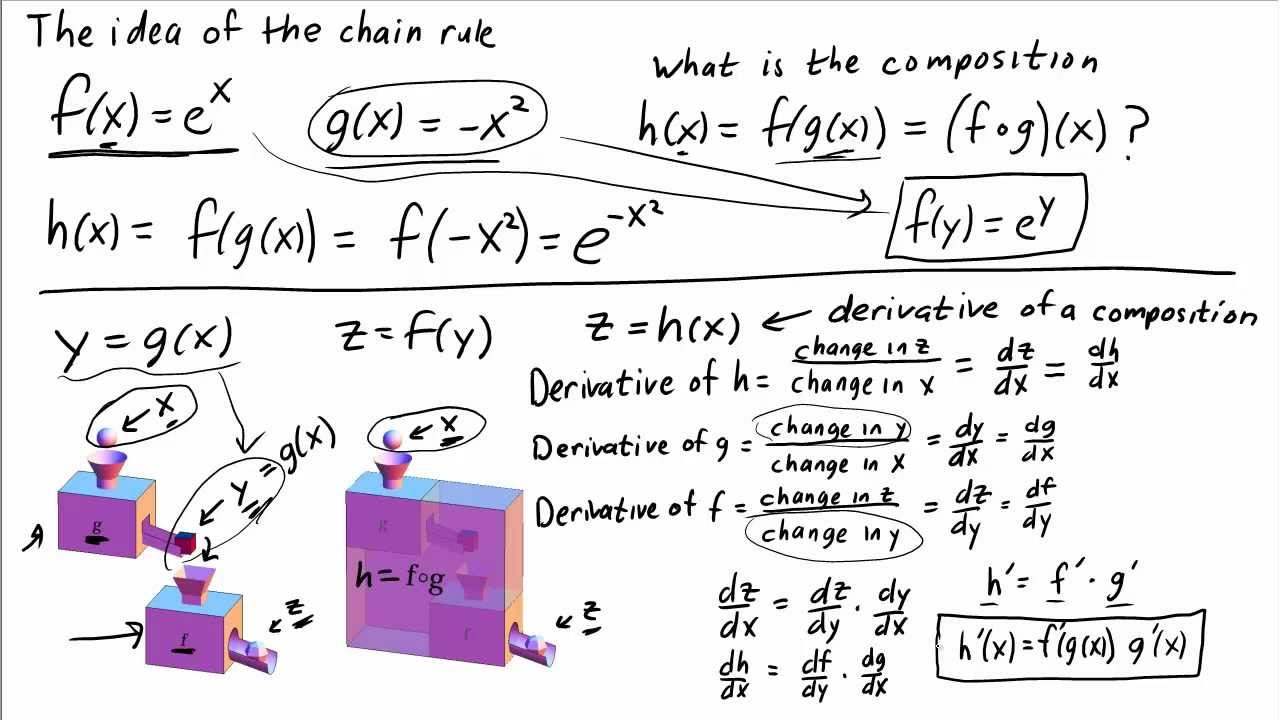



The Idea Of The Chain Rule Math Insight
Feb 11, 19 · \(\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{f'(a)}{g'(a)}\), if \(\lim_{x \to a} \frac{f(x)}{g(x)}\) gives the form 0/0 Where, f(a)=0 and g(a)=0 Limits of Exponential and Log Functions \(\lim_{x \to 0} e^{x}=1\) \(\lim_{x \to 0} \frac{e^{x}1}{x}=1\) \(\lim_{x \to \infty } \left ( 1\frac{1}{x} \right )^{x}=e\)According to the composition law, we have $$\lim\limits_{x \to 0}lnf(x) = ln\lim\limits_{x \to 0}f(x) = lnc$$ Because $\lim\limits_{x \to 0}g(x) = d$, we have $$\lim\limits_{x\to 0}g(x)lnf(x) = \lim\limits_{x\to 0}g(x)\cdot\lim\limits_{x \to 0}lnf(x) = dlnc$$ Apply composition lawagain, we getLimit Law in symbols Limit Law in words 1 f x g x f x g x lim ( ) ( ) lim ( ) lim ( ) →x a →x a →x a = The limit of a sum is equal to the sum of the limits 2 f x g x f x g x lim ( ) ( ) lim ( ) lim ( ) →x a →x a →x a − = − The limit of a difference is equal to the difference of the limits 3 cf x c f x lim ( ) lim ( ) →x a →x a




Continuity And Ivt




If Lim X To A F X G X Exists Then Which One Of The Fo
May 02, 16 · Following are two of the forms of l'Hopital's Rule THEOREM 1 (l'Hopital's Rule for zero over zero) Suppose that lim x → a f ( x) = 0 , lim x → a g ( x) = 0 , and that functions f and g are differentiable on an open interval I containing a Assume also that g ′ ( x) ≠ 0 in I if x ≠ a Then so long as the limit is finite, ∞, orHomework 5 Solutions 3132 f(x;y)=œ xy(x2−y2) x2y2 (x;y)≠(0;0) 0 (x;y)=(0;0) Note fis continuous, (by computing lim(x;y)→(0;0) of the formula above, eg using polar coorinates) (a) Find f x and f y when (x;y)≠(0;0) Away from (0;0);fcan be di erentiated using the formulaF(x n)g(x n) → f(a)g(a), which tells us that f g is continuous at a The composite function g f is defined by (g f)(x) = g(f(x)) for each x Suppose f is continuous at a and g is continuous at f(a) Let x n → a then since f is continuous at a we have f(x n) → f(a) But g is continuous at f(a) so g(f(x n)) → g(f(a)) ie, (g f)(x




Calculus Derivatives And Limits Tool Eeweb Community




How Solve Limit Of Lim X Gta F X G X Youtube
F(t)dt = f(x) This proves that g0(x) = lim h!0 g(x h) g(x) h = lim h!0 1 h Z xh x f(t)dt = f(x) Example Find the derivative of the functions listed below g(x) = Z x 1 p 9 t2dt;Nov 10, · Step 1 The function f(x) = x2 − 3x 2x2 − 5x − 3 is undefined for x = 3 In fact, if we substitute 3 into the function we get 0 / 0, which is undefined Factoring and canceling is a good strategy lim x → 3 x2 − 3x 2x2 − 5x − 3 = lim x → 3 x(x − 3) (x − 3)(2x 1) Step 2 For all x ≠ 3, x2 − 3x 2x2 − 5x − 3 = x 2x 1Lim x → a (f(x) ± g(x)) = A ± B = lim x → a f(x) ± lim x → a g(x) As with the product, it is not always possible to use that formula with infinite limits An expression, ∞ ∞ (in the sense of the difference of limits) may happen to evaluate to ∞, a finite number, or ∞ depending on the two limits involved




I M Completely Lost On The Limit In Number 8 How Can The Derivative Fit Into The Equation Askmath



Solved Given F X X 2 X And G X 3x 2 1 Use The First Principles Definition To Show F 5 G 1 Course Hero
If the existing limit is finite and having its x approaches for f (x) and for the same g (x), then it is the product of the limits A function f (x) usually contains the value of x but it is not compulsory Its best example is if f (x) = (x 4) (x 6)/2 (x 6)In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions Let f(x)=g(x)/h(x), where both g and h are differentiable and h(x)≠0In the same way, in textbooks and when writing things out, we use different function names like f (x), g(x), h(x), s(t), etc, to keep track of, and work with, more than one formula in any single contextWith function notation, we can now use more than one function at a time without confusing ourselves or mixing up the formulas, leaving ourselves wondering "Okay, which ' y ' is this one?"




Ppt Algebra Of Limits Powerpoint Presentation Free Download Id




Limit Of Function F X And G X From Given Limit Youtube
H(x) = Z x 5 1 p 1 cos2 t dt Note A careful look at the proof of the above theorem shows that it also applies to the situation where a x b If f is a continuousJul 23, 19 · For limits, we put value and check if it is of the form 0/0, ∞/∞, 1 ∞ If it is of that form, we cannot find limits by putting values We use limit formula to solve it We have provided all formulas of limits like Limits of Trigonometry Functions Limits of Log and Exponential Functions Limits of the form 1 ∞ and x^n FormulaLim x → a f (x) g (x) = f (a) g (a) \lim_{x\to a} \frac{f(x)}{g(x)} = \frac{f(a)}{g(a)} x → a lim g (x) f (x) = g (a) f (a) This is an example of continuity, or what is sometimes called limits by substitution Note that g (a) = 0 g(a)=0 g (a) = 0 is a more difficult case;




Ex 13 1 26 Find Lim X 0 Where F X X X 0 Teachoo




Chapter 8 Differential Calculus Pdf Free Download
Math 151 Study List Use the limit definition of a derivative to find the derivative 1 f(x) = x2 2x Solution f′(x) = lim h→0 f(xh)−f(x) h =lim h→0 (xh)22(xh)−(x2−2x)h =lim h→0 x22xhh22x2h−x22x h =lim h→0 h22xh2h h =lim h→0 h(h2x2) h =lim h→0 (h2x2)= 02x2 = 2x2 2 g(x) = x3 2 SolutionIntuitive Definition of a Limit Let's first take a closer look at how the function f(x) = (x2 − 4) / (x − 2) behaves around x = 2 in Figure 221 As the values of x approach 2 from either side of 2, the values of y = f(x) approach 4 Mathematically, we say that the limit of f(x) as x approaches 2 is 4F(x;y) = L and lim (x;y)!(x0;y0) g(x;y) = K then lim (x;y)!(x0;y0) f(x;y) g(x;y) = L K lim (x;y)!(1;0) x2 2y 3 x y =?




Answered Substituting The Simplified Numerator Bartleby




Limits By Factoring Video Khan Academy



towne105review1 Jpg




Solved Contrary To What The Exercise Says Do Not Use Exe Chegg Com



Solved Math 115 Exam 1 February 12 19 Page 6 5 15 Points Below Is A Portion Of The Graph Of An Odd Function F X And The Formula For A F Course Hero




Calculus




The Quotient Rule Derivativeit




Limit Laws And Evaluating Limits Owlcation




Ap Calculus Ab Final Exam Review Semester 1 16 Derivative Space
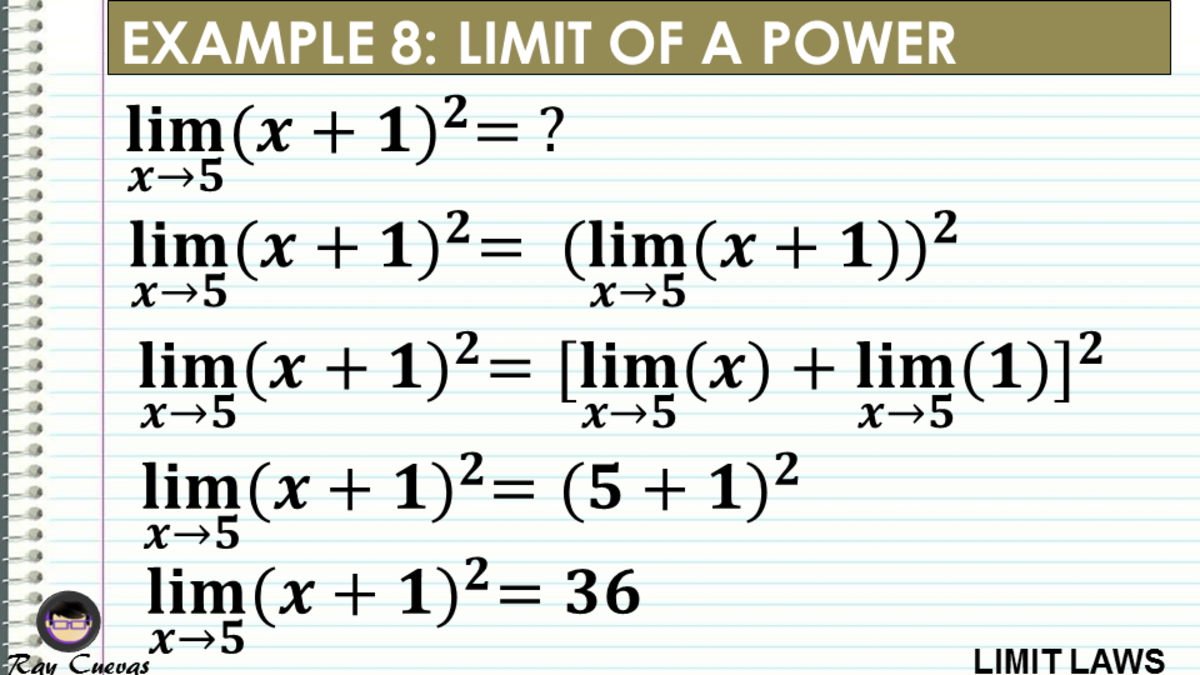



Limit Laws And Evaluating Limits Owlcation




Solved Explain What Is Meant By The Equation Lim F X 8 Chegg Com




The Third Calculus Competition Of Uw La Crosse




Limits And Derivatives Formulas Derivative Mathematical Relations




Limits Formula Pdf Math Formulas




Given The Function Gx Frac 1 Square Root Of X Fi Gauthmath



Calculus Index Cards
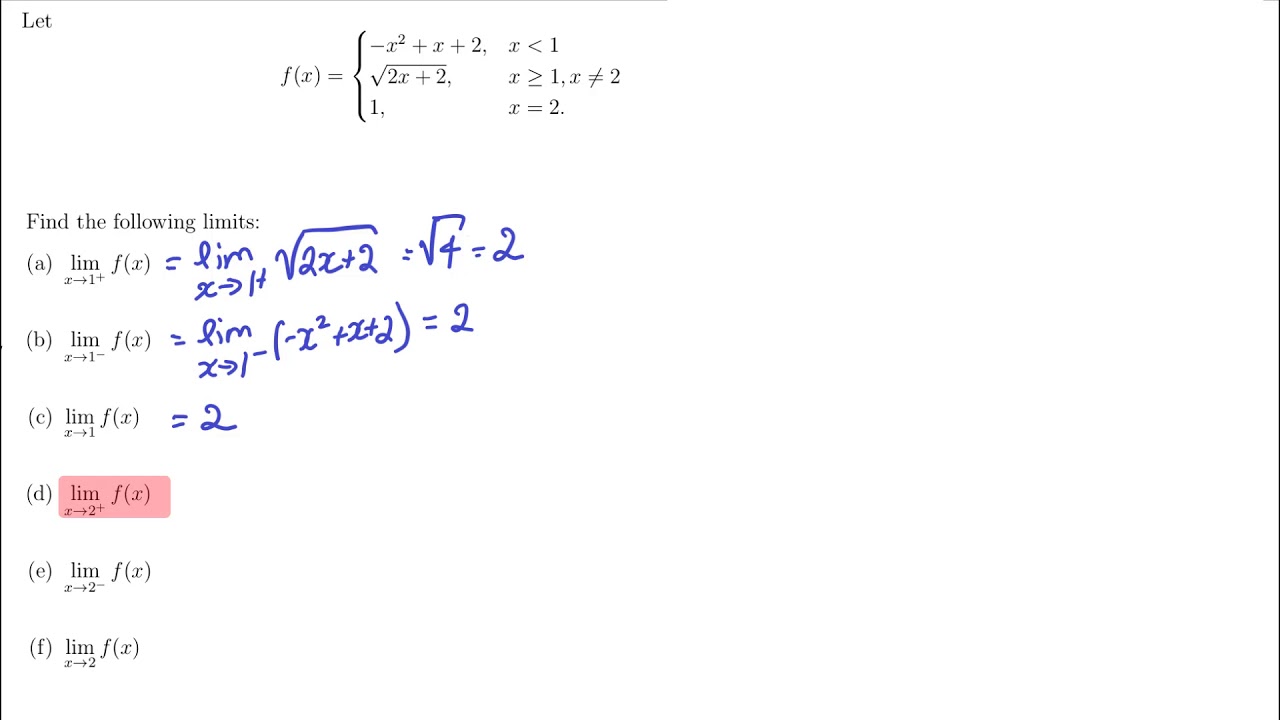



Computing Limits Algebraically




If G X Sqrt 25 X 2 Find The Value Of Lim X 1 G X G 1




Proof Of Taylor S Theorem Mathematics Stack Exchange




Theorem For Limits Of Composite Functions Video Khan Academy




Exploring The Derivative Of The Exponential Function Math Insight




Preparing Precalculus Preparing Precalculus Sheet Help In Academic Math




Derivative Of F X 1 X Using The Limit Definition Youtube




Solved X0u W Uive Possible Formulas For F X And G X If Chegg Com




Limit Laws Utrgv




11 Problems On Derivative Functions Exam 1 Math 1441 Docsity
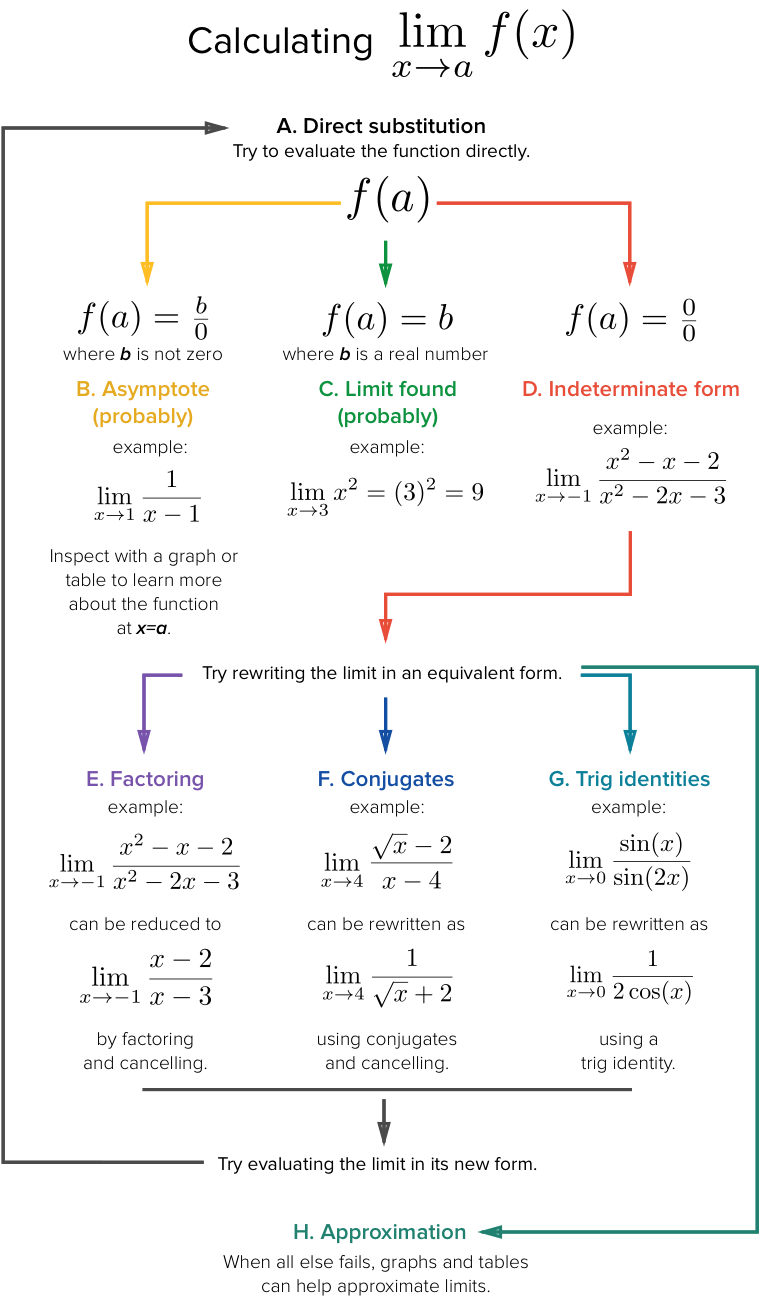



Strategy In Finding Limits Article Khan Academy




Limits Using Algebraic Manipulation By Can Balkaya Betamat En Medium



0 件のコメント:
コメントを投稿