Tan2x = 2tanx/ 1 tan²x What is the value of sin 225 degree?LS=3732 RS=3732 Yes, if the term at the bottom is tan^2 x, you typed tan^x, and I read it as tan x I got the proof, give me a bit of time to type it I'm sorry Mr Reiny you are right it is tan^2x LS= 2tanx/ (1tan^2x) 1/ (2cos^2x 1) = 2sinx/cosx 1/ (1sin^2x/cos^2x) 1/ (2cos^2xProduct identities function between any two functions is equal to those two functions being multiplied, eg, tan and cos multiply to sin OR for two functions opposite each other, their product is equal to one eg, tan and cot reciprocal identities can be found by going through the one, eg, sin to csc is 1/csc

212 8 4 8 S 1 2 Tanx Tanx Sec X Dx A Log S Math
What is 1+tan^2x equal to
What is 1+tan^2x equal to-Solutions are x = 675 ∘ and x = − 225 ∘ So 2 x is either 135 ∘ or − 45 ∘, and the tangent is − 1 QED Share answered Oct 15 '13 at 242 DJohnM DJohnM Both answers above are incomplete `tan^2x=tanx` `tan^2xtanx=0` `tanx(tanx1)=0` `tanx=0` implies that `x=0kpi` where k is an integer(Or `k*180^@` if




If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2 Youtube
4 cos 2 (4 π − 2 x ) 4 sin 4 x sin 2 2 x is always equal to View solution If 1 lies between the roots of the equation 3 x 2 − 3 sin a − 2 cos 2 a = 0 , thenThe trigonometric identity `(tan^2x)/(1tan^2x) = sin^2x` has to be proved Start with the left hand side `(tan^2x)/(1tan^2x)` Substitute `tanx = sin x/cos x` Can tan theta equal 2?
This all seems too complicated Solve the quadratic in tan ( x) and use the tan − 1 button; Tan^2 x1=sec^2x So to get 1 on the other side of the equal sign wouldn't it be sec^2xtan^2x=1?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!1 A water molecule is held together by two single polar covalent bonds False 2 Because oxygen has a greater electronegativity than hydrogen, water molecules are polar withWell, since tan (A B) = sin (AB)/cos (AB), we can use the sum formulas of sin (AB) and cos (AB) to yield that tan (AB
Answer to LHS= Tan(3x)=3tanxtan^3x/13tan^2x=RHS =tanx(2tanx/1tan^2x)/1Tan^2x(2tanx/1tan^2x) =2 tanxtanx(1tan^2x)/1tan^22Proof of the doubleangle and halfangle formulas Trigonometry from the very beginning The doubleangle formulas are proved from the sum formulas by putting β = We have 2 sin cos cos 2 − sin 2 (1) This is the first of the three versions of cos 2 To derive the second version, in line (1) use this Pythagorean identityIntroduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula




Exercise 1 Hy 100 1 X Tw 1 Then Content 17 2 If Y Log Vcosx
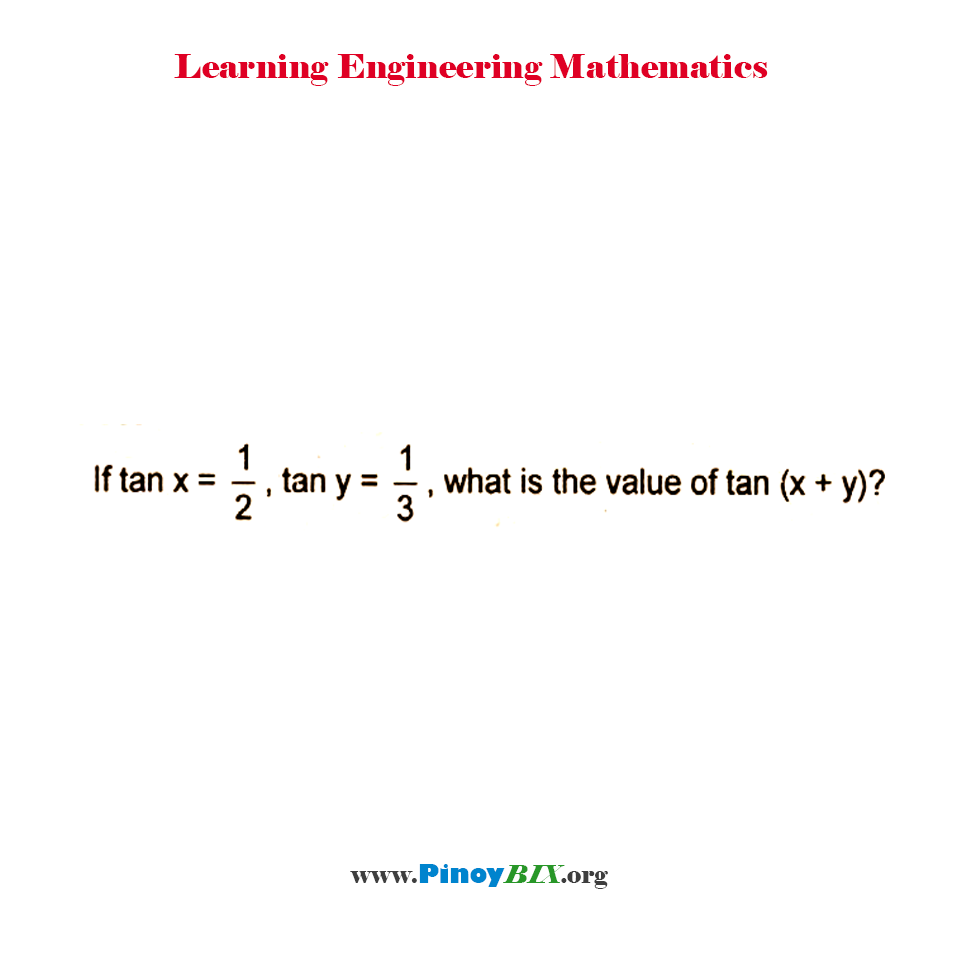



Solution If Tan X 1 2 Tan Y 1 3 What Is The Value Of Tan X Y
f(2tanx/1tan 2 x)=(cos2x1) (sec 2 x2tanx)/2 then f(4) is equal to? Find an answer to your question if 2tanx/1tan^2x=1, then x can equal michaelbarnesa michaelbarnesa Mathematics High School answered If 2tanx/1tan^2x=1, then x can equal 2 See answers hartnn hartnn Tan 2x = 2 tan x / (1tan^2x) hence, tan 2x = 1 2x = pi x = pi/2Use the formulae> tan(2x)= 2tanx/1tan^2x to solve it 0 reply fudgesundae Badges 16 Rep?




Lim X Tan 1 3 Tan 2x 2 Tanx 3 Tan 2x 4 Tanx 3 Where Is Greatest Integer Function Of X




Sec 2 2x 1 Tan2x Youtube
The first solution is 45° more than a multiple of 180°, so (180n)° 45° should do The second solution is 30° more than a multiple of 180° and (because of the "plus / minus") also 30° less than that same multiple, so (180n)° ± 30° will cover this part(2tanx / (1 tan 2 x)) = 1 Recall Trigonometry formulas tan2A = (2tanA / (1 tan 2 A)) Substitute (2tanx / (1 tan 2 xTan(2x) as tan(xx) So tan(2x)= 2tanx/1tanxtanx We can always go for the longer approch from sinx/cosx to derive this formula




Graph Of Y Tan X Video Trigonometry Khan Academy




0 Xlimc 1 1 Dfractan3x 2tan See How To Solve It At Qanda
Prove Sin2x 2tanx 1 Tan 2x Socratic cos2x=(1tan^2x)/(1tan^2x) =(1tan^2x)/sec^2x =(1tan^2x)cos^x =cos^xsin^x =cos2x\begin{align} 1^2 tan^2x = sec^2x \quad 1^2 cot^2x = csc^2x \end{align} Proof of Pythagorean Trigonometric Identity Equivalencies We will not prove the unit circle trigonometric identity because it is already geometrically proven on Use tan x=sinx/cos x, sin 2x = 2 sin x cos x and cos 2x = cos^2xsin^2x, for the right hand side expression 2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x) =2 sin x cos x/(cos^2xsin^2x) =(sin 2x)/(cos 2x)=tan 2x Proofs for sin 2x = 2 sin x cos x and cos 2x = 1 2 sin^2x Use Area of a triangleABC = 1/2(base)(altitude) = 1/2 bc sin A Here, it is the triangle ABC of a unit circle,Important Angle Summary Is 1 tan 2x an identity?




A Solution Of The Equation 1 Tan X 1 Tan X Sec 2x 2 Tan 2 0 Where X Lies In The Interval Pi2 Pi2 Is Given By




Cosec 1 1 Tan 2 X 2tanx
Since we know by the double angle formulae that tan2X = (2tanX)/ (1−tan^2X), we see as follows tan2 (AB) = 2tan (AB)/ (1tan^2 (AB)) Now, if we can determine what tan (AB) equals, our life would be much easier!Tap for more steps Set the first factor equal to 0 0 tan ( x) 2 = 0 tan ( x) − 2 = 0 Add 2 2 to both sides of the equation tan ( x) = 2 tan ( x) = 2 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent x = arctan ( 2)Sin(2X) = 2 sinX cosX cos(2X) = 1 2sin 2 X = 2cos 2 X 1 tan(2X) = 2tanX / 1 tan 2 X Multiple Angle Formulas sin(3X) = 3sinX 4sin 3 X cos(3X) = 4cos 3 X 3cosX sin(4X) = 4sinXcosX 8sin 3 XcosX cos(4X) = 8cos 4 X 8cos 2 X 1 Half Angle Formulas




212 8 4 8 S 1 2 Tanx Tanx Sec X Dx A Log S Math




Which Of The Following Are Solutions To 2tanx 1 Tan 2x Sqrt 3 Check All That Apply Options Are In Brainly Com
If(2tanx/(1tan^2x))=1, then x can equal? Tan2x=2tanx/1tan^2x Stepbystep explanation Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functionsYou get these gems as you gain rep from other members for making good contributions and giving helpful advice nope, the simple way is to rewrite tan2x as sin2x/cos2x then integrate by substitution I get the answer as 1/2 ln (cos2x) c




Difficult Round 15 Area Circle




Trigonometric Functions Pages 1 Flip Pdf Download Fliphtml5
Share with your friends Share 0 Each question has four choices a,b,c and d out of which only one is correct Each question contains Statement 1 and Statement 2 Make your answer as If both the statements are true and Statement 2 is the correct explanation of statement 1 If both the statements are True but Statement 2 is not the correct explanation of Statement 1 If Statement 1 is True and Statement 2 F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2 How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic Some trigonometric identities follow immediately from this de nition, in particular, since the unit circle is all the points in plane with xand ycoordinates satisfying x2 y2 = 1, we have cos2 sin2 = 1 Other trignometric identities re ect a much less




Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube



2
I understand the trig function involved if it's just (2x) and tan is not squared @Tyrion101, despite what others have said in this thread, yes, tan 2 ( 2 x) is the square of tan ( 2 x) Tyrion101 said But is it equal to (2tanx/1tan^2x)^2 is what I'm asking I may have been unclear But, since the cosine is always less than or equal to 2, we see that the statement tex\cos(2x)=2/tex cannot have any solutions at all (that is, whatever number "x" you substitute into the expression on the lefthand side, will never make cos(2x) equal to 2 8 \frac{2 tan ~x}{1tan^2 x} =\frac{1}{\sqrt{3} } \\tan ~2x=tan~30,tan~210,tan~ (),tan~()\\2x=30,210,390,570\\x=15^\circ,105^\circ,195^\circ,285^\circ zaniahsims zaniahsims Answer




If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2 Youtube




Prove That Tan2x 2tanx 1 Tan 2x Youtube
Pythagorean identity equal to csc^2(x) 1 cot^2(x) Reciprocal identity equal to csc(x) 1/sin(x) Reciprocal identity equal to sec(x) 1/cos(x) Reciprocal identity equal to cot(x) Tan(2x) = (2Tanx) / (1 Tan^2x) area of a triangle K = 1⁄2ab sinC K = 1⁄2bc sinA K = 1⁄2ac sinB sin 30 1/2 sin 45 √2/2 sin 60 √3/2 sin 0 0 sinLHS=tan{(2x)} =tan(xx) We know that tan (A B)= tan(A)tan(B) / 1 tan A tan B Applying the same formula we get =>tan(xx)= tan(x)tan(x) / 1 tan xIf (2tanx)/(1tan^2 x)=1/sqrt3, then x can be equal to _____ (check all that apply) a) x=5pi/12 npi b) x=7pi/12 npi c) x=11pi/12 npi d) x=pi/12 npi
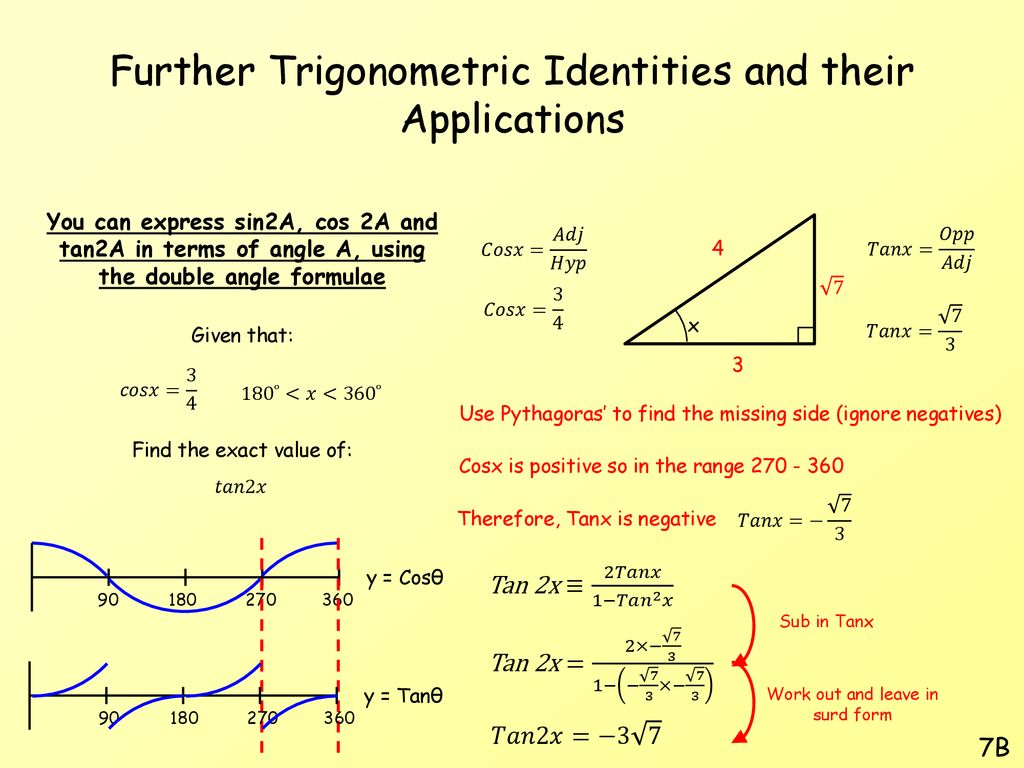



Further Trigonometric Identities And Their Applications Ppt Download




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco
If x = 30°, verify that (i) tan 2x= (2tan x)/ (1tan ^2x) Mathematics I need to prove that the following is true Thanks (2tanx /1tan^x)(1/2cos^2x1)= (cosxsinx)/(cosx sinx) and thanks check your typing I tried 30º, the two sides are not equal$\endgroup$ – Black Crescent Apr 18 '15 at 1627 Show 2 more comments 1




The General Solution Of The Equation Tanx Tan2x Tanx Tan2x 1 Is Youtube




Ex 7 2 25 Integrate 1 Cos 2 X 1 Tan X 2 Ex 7 2
L7B 26D 2 Given these numbers 2 in, 1 in, 8 in, what can we find out using the triangle ineA The numbers can be the measures of the sides of a triangleB The sum of any two numbers determines the length of the third sideC The sum of the two smallest numbers is less than the third sideD The sum of the two smallest numbers is equal toJEE Main 75% criteria exempted for NITs, IIITs admissions as well Know the extended last date of registration, exam eligibility, syllabus reduction & etc for JEE main 21Solve for x tan (2x)= (2tan (x))/ (1tan (x)^2) tan (2x) = 2tan (x) 1 − tan2 (x) tan ( 2 x) = 2 tan ( x) 1 tan 2 ( x) Since x x is on the right side of the equation, switch the sides so it is on the left side of the equation 2tan(x) 1− tan2(x) = tan(2x) 2 tan ( x) 1 tan 2 ( x) = tan ( 2 x) Simplify the denominator




If Log3sin X Log3cos X Log3 1 Tan X Log3 1 Tan X 1 The Tan 2x Is Equal To




Lim X 0 1 Sin 2x 1 3 1 2tanx 1 4 Sinx Tan 2x
What is the value of Tan 2 theta?This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Confirming that the result is an identity not sure how to start this one, i have tried it a few different ways and i still can't get it (1 tanx)^2 = sec^2x 2tanx




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




By Siby Sebastian Pgt Maths Ppt Download
If r is equal to a costi asinti at tan alpha k then show dr /dt d 2 r/dt 2 d 3 r/ dt 3 =a 3 tan 1 Answer(s) Available Find the integration of the expression as per attachmentHere is what I have so far A) mu SOLUTION Verify this identity (tan^2 (x)1)/ (1tan^2 (x)) = 12cos^2 (x) I've started a couple different options but none are working out for me Here is what I have so far A) mu Algebra Trigonometry#10 Report 9 years ago #10 (Original post by ilovemath) na I see what I did wrong we CANNOT HAVE the reciprocal of 0 You can just do cos 2x/sin 2x = 0 So you know that cos 2x = 0 You should be able to get the other two solutions from that




Tan4 Yt0m0 3an28 0 1 To See How To Solve It At Qanda




F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2
we know tan2Q = 2tanQ / 1tan 2 Q using this formula, tan4x = tan2(2x) =2tan2x / 1tan 2 2x = 2(2tanx/1tan 2 x) / 1(2tanx/{1tan 2 x} 2) simplify to get , 4tanx(1tan 2Click here👆to get an answer to your question ️ Prove that tan 4x = 4tanx (1 tan^2x)1 6tan^2x tan^4x $\begingroup$ @lab bhattacharjee its in which way is 2tanx/1tan^2x 1/2cos2(x)−1 equal to tan2xsec2x?



Df0039 On Vimeo




Dx 2 If Y Log Vcosx Then Dy 1 Tanx 2 1 2tanx 3 Sinxcosx Ay
Sin (b) Cos (a)Cos (b) Therefore, sin (xx) = sin (x)cos (x) cos (x)sin (x) = 2 sin (x) cos (x) Also, Sin 2x = 2 t a n x 1 tan 2 x To Prove Sin2x in the form of tanx x which is equal to 2 t a n x 1 tan 2 x Now let us start the proof from the righthand side and hence, prove it as LHS = RHS Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers by




Tan2x 2tanx 0 Solve Giving The General Value Maths Meritnation Com




1 Tanx Tan X 2 Secx Tanx Cotx 2 1 Prove It Brainly In




Derivatives Of Tan X And Cot X Video Khan Academy



Web Auburn Edu Holmerr 1617 Textbook Lhopital Print Pdf




Www Mercadocapital Sec 2x 2 Tan 2x Trigonometric Identities



1




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Limit X Tends P 4 Sec 2x 2 Tanx 1 Brainly In
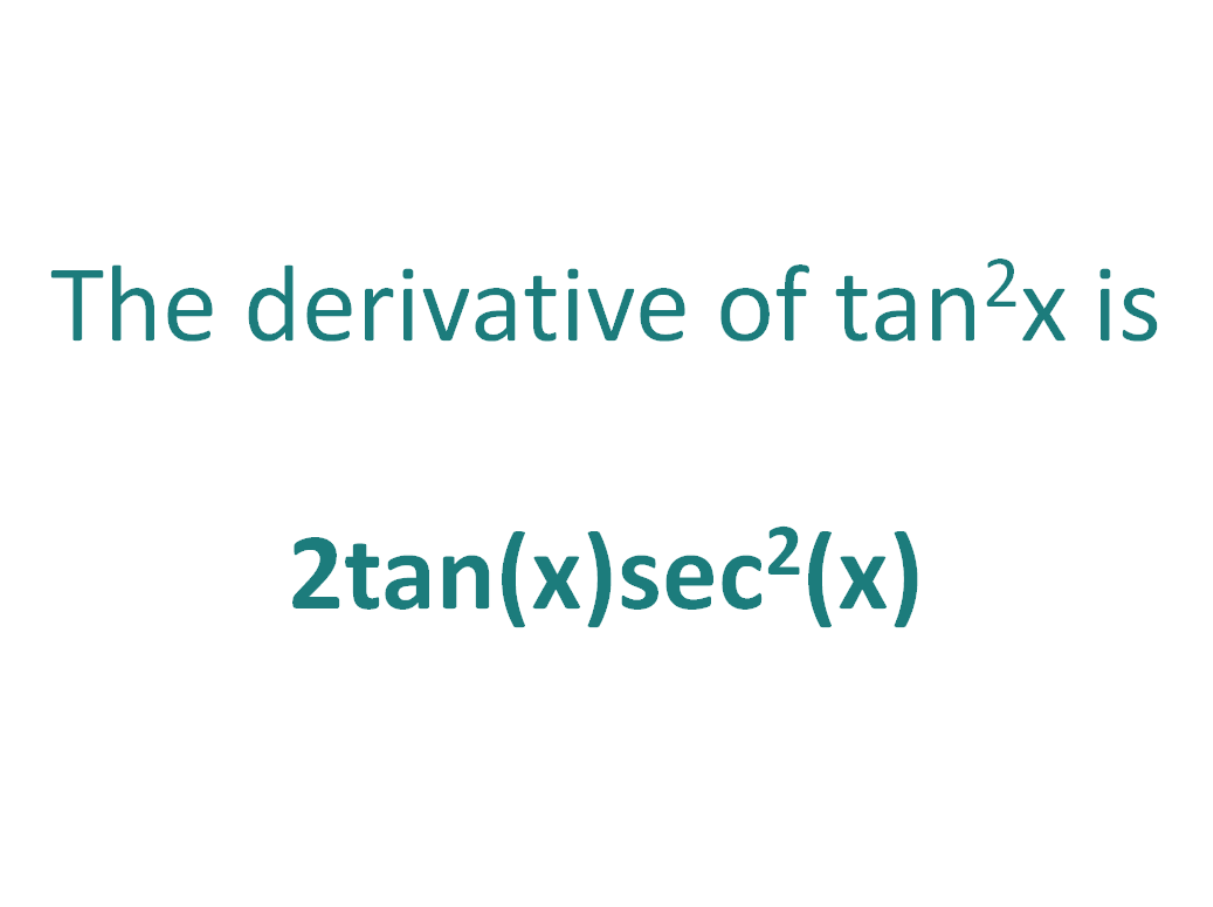



The Derivative Of Tan 2x Derivativeit



Www Houstonisd Org Cms Lib2 Tx Centricity Domain Precalc Unit 5 Soln Pdf




2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula



Tan 2x Tan 2x




Trig Limit 1 Tanx X Pi 4 Compound Angle Substitution Youtube




Ais Equal To A 3v5 Cos I V5 3 Is Equal To 3 5 V5 3 4 B Scholr
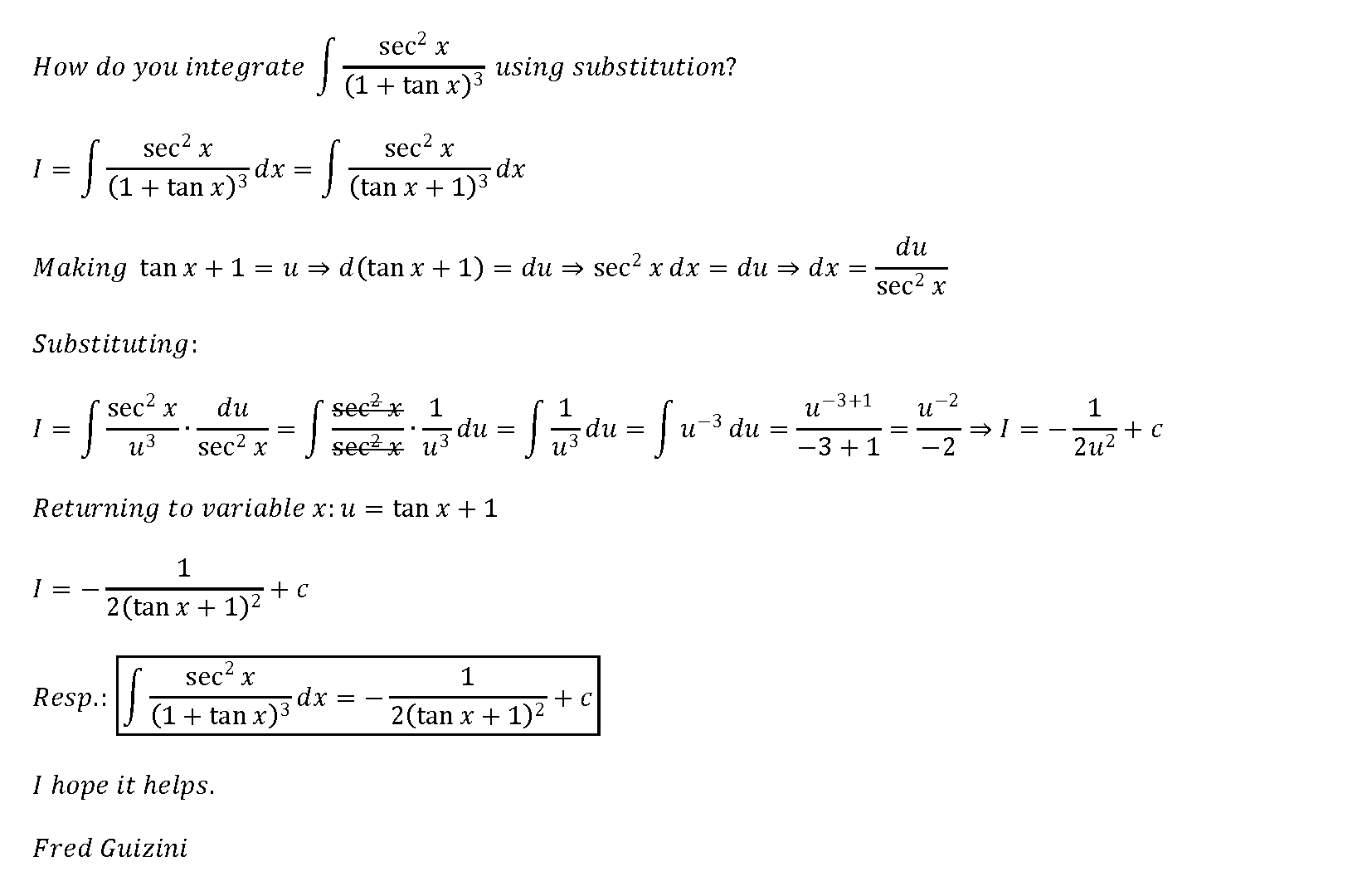



How Do You Integrate Int Sec 2x 1 Tanx 3 Using Substitution Socratic




Old Version Show Sin 2x 2 Sin X Cos X 2tan X 1 Tan 2 X Youtube



How To Solve Math Displaystyle Lim X To 0 Dfrac Tan X 4 Tan 2x 3 Tan 3x X 2 Tan X Math Quora




Trigonometric Identities Ppt Download



Www Rusdlearns Net C File Show




Prove That Tan2x 2tanx 1 Tan X Brainly In




Trigonometry Reciprocal Identities Expii



Www Jensenmath Ca Unit 5 pretest review solutions Pdf




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco
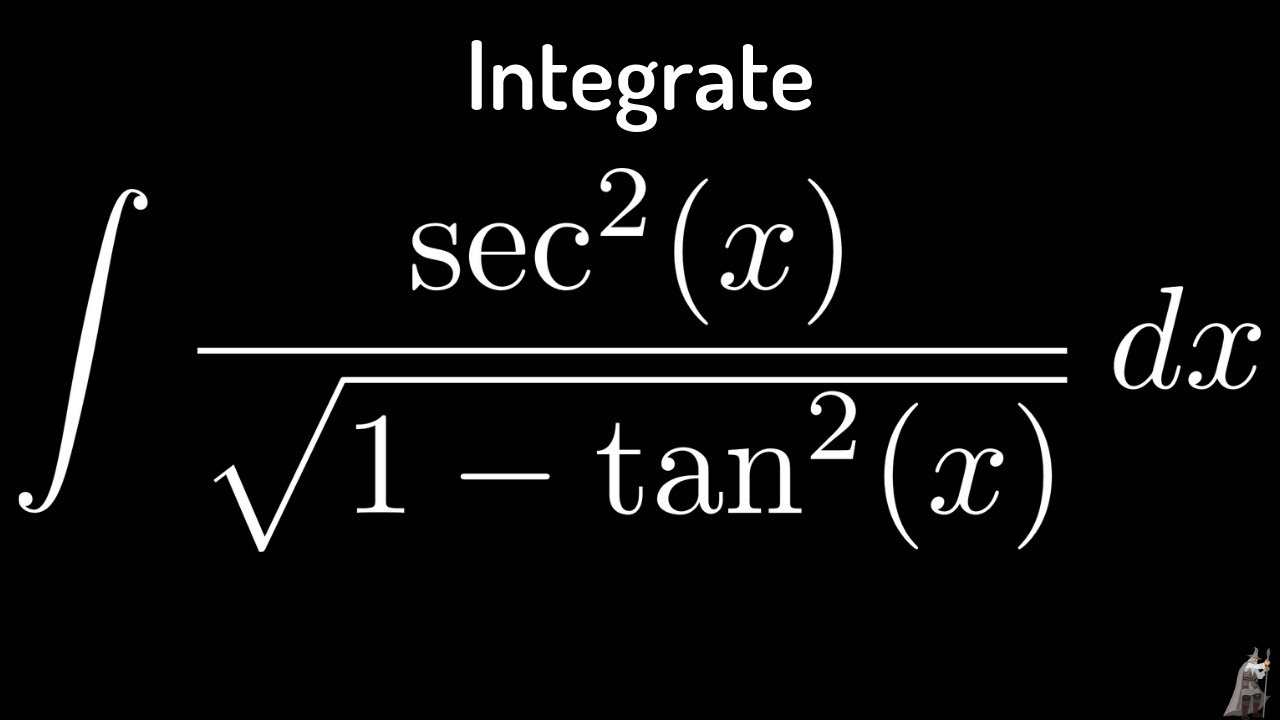



Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube




Answered Find Sin 2x Cos 2x And Tan 2x From Bartleby




Tan 2x Formula What Is Tan 2x Formula Examples




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



What Is The Integration Of 1 Tan 2x 1 Tan 2x Quora




If Y 2 Tan X 2 Prove That Dy Dx 2 1 Cosx Maths Application Of Derivatives Meritnation Com




Let Tan 2x 1 2tan 2 Y Then Prove That Cos 2y 1 2cos 2x




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2




Integration Calculus Notes



Answered 25 Bartleby




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2




Solve The Trigonometric Equation Tan X Tan 2x Tan X Tan 2x 1




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Integral 1 Tan 2 X Sec 2 X Youtube




The Value Of Lim X Gt0 Xtan2x 2xtanx 1 Cos2x 2 Is Equal To Youtube



Www Thatonemathguy Com Uploads 7 0 1 3 Precalculus 2nd Edition Part 2 Pdf




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco



Search Q Trig Identities Tbm Isch




If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2




Differential Equation D 2 1 Y E X Sec 2 X Tan X Mathematics Stack Exchange




Misc 9 Cos X 1 3 Find Sin X 2 Cos X 2 And Tan X 2




How Do You Solve Sec 2x 2tanx 0 Socratic




Integral Of 1 Tan 2x 2tan X Brainly In




Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2



Ovingtonclassroom Weebly Com Uploads 1 0 6 2 Chapter 4 Review Key Pdf




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




In Exercises 1 6 Verify That Each X Value Is A Chegg Com



Boitz Weebly Com Uploads 2 5 6 5 Key 4 2 Pdf




Lim X To 0 2 Tan X 2 Sin X X 2 Sin X Without L Hopital S Rule How Is My Procedure Wrong Mathematics Stack Exchange




If Tanx Tan 2x 1 Then The Value Of Tan 4x 2 Tan 3x Tan 2x 2 Tanx K 4 Then K Is Equal To



How Do You Solve Sec 2x 2tanx 0 Socratic




Tan2x ただの悪魔の画像



3



Q Tbn And9gcrzz4 1ds9ppsd8y 0vi 8exu9yrzt2issbxxz9kcs1yppfojoc Usqp Cau



How Do You Prove 2sin 2x 1 Sinxcosx Tanx Cotx Socratic




3 Simplifying Trig Expression 1 Tan 2x Youtube



Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf
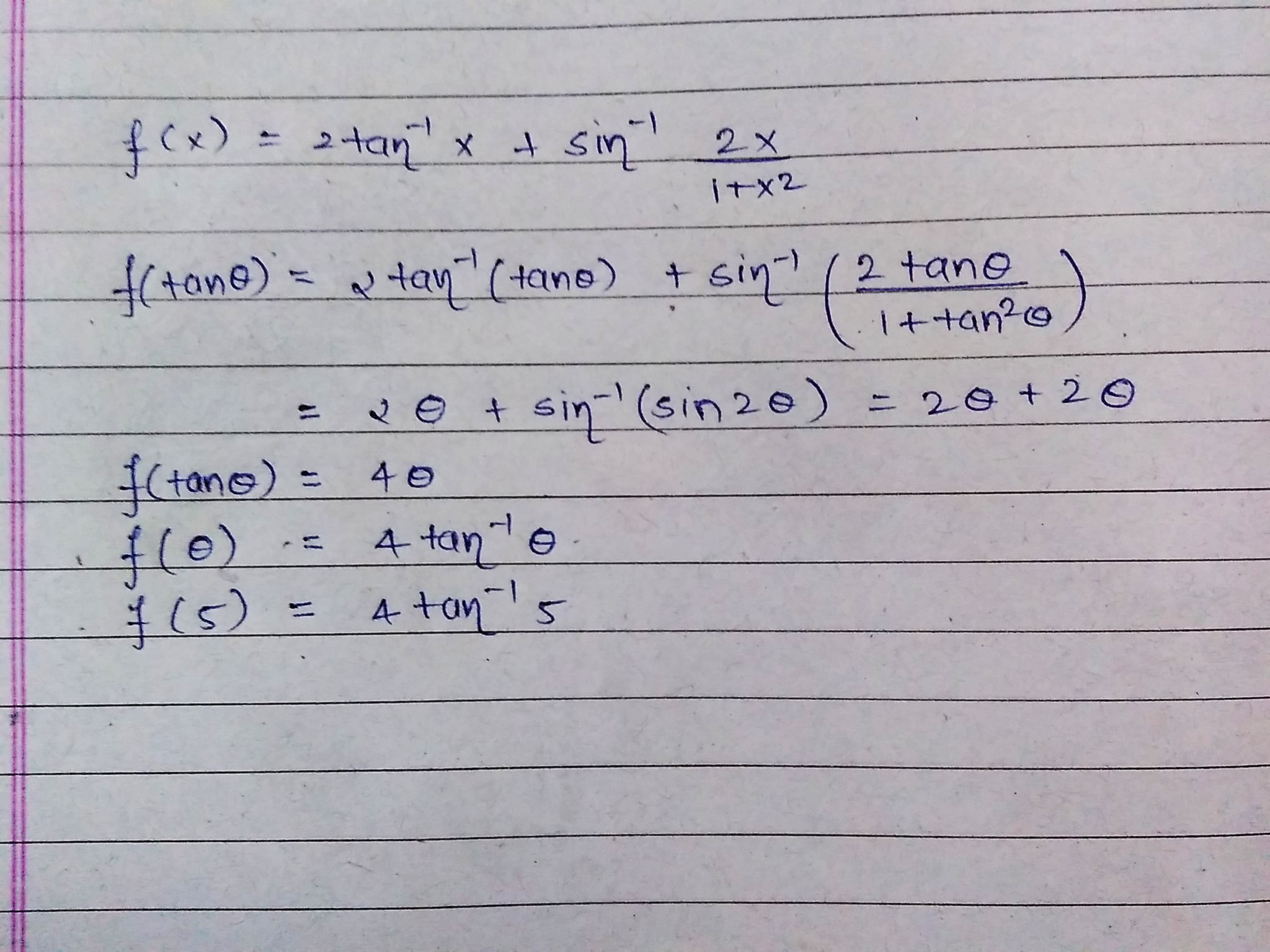



F X 2 Tan 1x Sin 1 2x 1 X 2 Then F 5




Tan 2x 2tanx 5dy Dx 2 1 Tanx Sec 2x Differential Equations Brainly In




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11




Misc 10 Sin X 1 4 Find Sin X 2 Cos X 2 Tan X 2 Chapter 3



The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0 Is Youtube




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Find The Values Of X In The First Quadrant Such That 2 Tan X 1 Tan X Is Positive Brainly In




Evaluate Lim X Tan 1 3 Tan X 2tanx 3 Tan X 4tanx 3
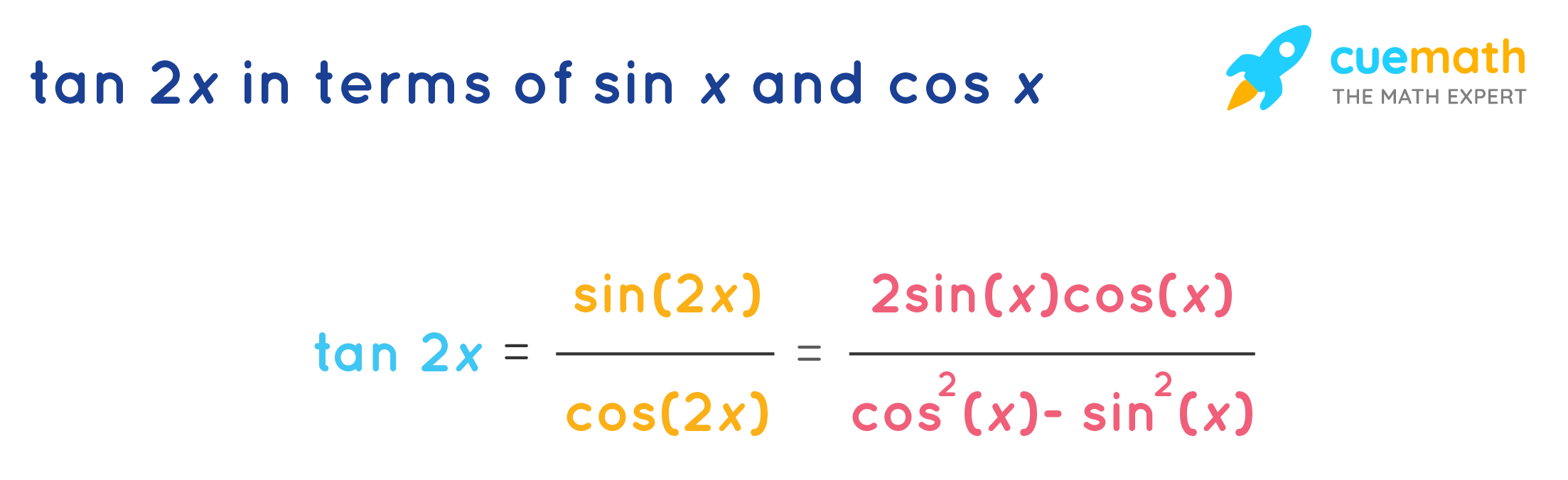



Tan 2x Formula What Is Tan 2x Formula Examples




Solve Sinxtanx 1 Tanx Sinx




Lim X Tends To Pi 4 Sec 2x 2 Tanx 1 Brainly In



Http Ww2 Justanswer Com Uploads Ryanp97 12 04 05 Solutions3 Pdf



How To Show That Sec X Tan X 1 Sec X Tan X Quora



How To Prove The Identity In Tanx Cotx 2 Sin2x Quora




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11




Integration Calculus Notes



0 件のコメント:
コメントを投稿